Solution Notes (Mark Gordon): This problem was a bit unusual due to the nature of the intended solution. At least one competitor got the basic idea and several observers managed to score full points.

The first thing to notice about the problem is that it's describing a perfect binary AND/OR tree. In this case our tree is rooted with an OR node and alternates between AND and OR operations each level. The leaves then are true or false and determined by some function of their position in the tree. Below is a picture of the tree generated by the sample input. Nodes that evaluate to true (i.e. the cows can come home) are shown in green and nodes that evaluate to false are shown in red. The left child corresponds to to choosing the bottom half of cards and the right child the top half.

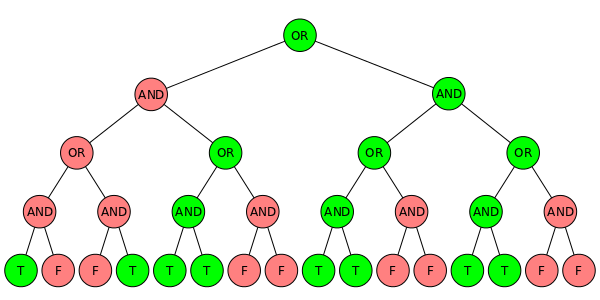
To find the lexicographically smallest solution for John we should always try and choose to bottom half of cards if possible. Otherwise we must follow the 'top' branch instead. After determining the choice for John we then make the choice required for Bessie at each level. Below is a sketch of this idea:

x = root
for i = 1 to N
  if evaluate_tree(x.B)
    x = x.B
  else
    x = x.T
  if bessie_moves[i] = 'B'
    x = x.B
  else
    x = x.T

So now we need to write the function 'evaluate_tree'. At first glance it looks impossible to compute this function in better than O(4^N) time without looking into the structure of the tree. However, this is not the case.

The crux of the solution is that we can use the concept of short circuiting to avoid evaluating certain subtrees entirely. Indeed because 'false' short circuits AND and 'true' short circuits OR it seems likely we'll be able to take advantage of this a lot. If you got this far you got most of the points for this problem.

However, the input specification is not as random as it appears. Given whether you evaluate the 'B' or 'T' subtree first there was test data designed so that short circuiting never helps you. Not to worry, though. Simply randomizing the order you visit subtrees is enough to correct this problem and provably reduce evaluate_tree's asymptotic runtime.

To prove the algorithm's runtime we should first use De Morgan's law to see that if we interchange AND and OR, flip the leaves, and flip the output value we have the same logical expression. Therefore it's enough to analyze the tree assuming you're always rooted at an OR node (as is the case for John). Let f(d) give the expected runtime of the worst case input if the subtree evaluates to 'false' and let t(d) be similar for 'true'.

In the false case we will have to evaluate both subtrees no matter what so f(d) = 2 * t(d - 1) [Note the application of De Morgan]. In the true case we do the most work when only one child is 'true' which we must evaluate every time. The other 'false' node is evaluated half the time. Therefore t(d) = f(d - 1) + 1/2 * t(d - 1). Substituting our result for f(d) we get the recurrence t(d) = 2 * t(d - 2) + 1/2 * t(d - 1). Solving the recurrence shows that t(d) = ((1+sqrt(33)/4)^d ~ 1.68614066^d.

In our case 2 * N = d so our overall algorithm is O(2.84307033^N)! Because the cost of evaluation is shrinking exponentially as we generate the complete output it doesn't actually affect the asymptotic runtime. Below is my solution to this problem.

#include <iostream>
#include <cstdlib>
#include <cstdio>

using namespace std;

#define MAXN 14

int N, M, K;
string S;

int A[8 * MAXN];

int calc(int y, int x, int a, int b) {
  return (1ll * x * (A[y * 8 + a * 4 + b * 2] + 1) +
                     A[y * 8 + a * 4 + b * 2 + 1]) % M;
}

bool solve_and(int y, int x, bool a);

bool solve_or(int y, int x) {
  if(y == N) return x <= K || x + K >= M;
  bool mv = rand() & 1;
  return solve_and(y, x, mv) || solve_and(y, x, !mv);
}

bool solve_and(int y, int x, bool a) {
  bool mv = rand() & 1;
  return solve_or(y + 1, calc(y, x, a, mv)) &&
         solve_or(y + 1, calc(y, x, a, !mv));
}

int main() {
  freopen("cowrun.in", "r", stdin);
  freopen("cowrun.out", "w", stdout);

  cin >> N >> M >> K;
  cin >> S;
  for(int i = 0; i < 8 * N; i++) {
    cin >> A[i];
  }

  int x = 0;
  for(int i = 0; i < N; i++) {
    if(solve_and(i, x, true)) {
      cout << 'B';
      x = calc(i, x, true, S[i] == 'B');
    } else {
      cout << 'T';
      x = calc(i, x, false, S[i] == 'B');
    }
  }
  cout << endl;
}