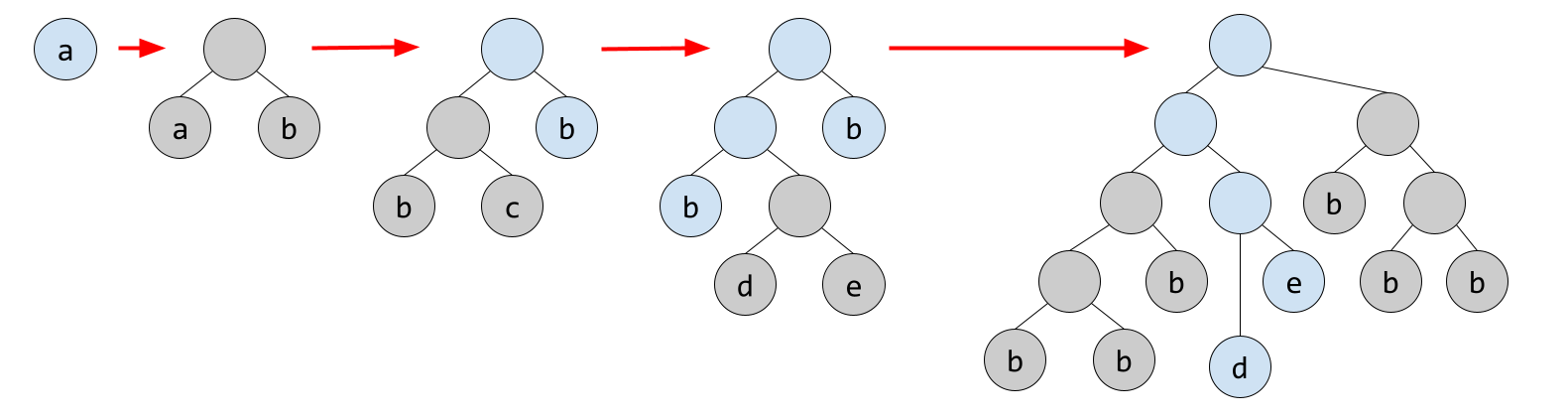
A natural data structure to represent the string $S$ is a binary tree where each leaf node contains an individual character and an operation involves replacing some leaf nodes with subtrees. For instance, the tree corresponding to the example input would evolve like so:

This data structure is helpful for printing out the answer because we can easily and efficiently prune large branches off the tree until we're only left with what we want. We can do this by storing the size of each subtree in its root node.
However, the final string may be upwards of $2^{100000}$ characters long, so constructing the tree explicitly is out of the question. It helps to take a step back and ask, how can the string get so long? In this case, $S$ gets long when it contains many occurrences of one letter that get replaced with a longer string $s$. This results in $s$ appearing many times in $S$ and, as a result, many identical subtrees being appended to the tree.
Storing all of these identical subtrees explicitly would be extremely inefficient; a better idea would be to store only one instance of the subtree and then replace the affected leaves with pointers to that instance. We can illustrate this using the example input again:
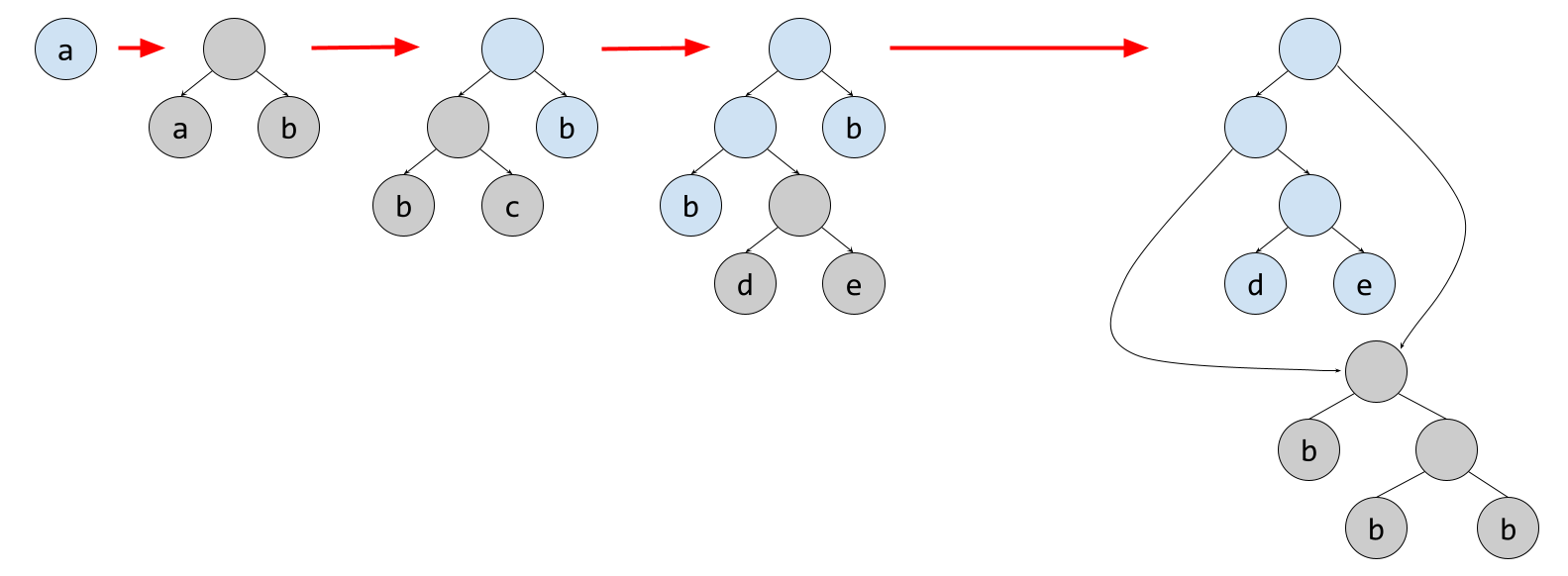
This solves the problem of fitting everything into the available memory, but we still have another problem to deal with. Iterating through each occurrence of some letter in $S$ and pointing each to the new subtree is also quite inefficient and difficult to implement.
To address this problem, we can try to construct the final tree from the leaves up. To do this, we must iterate through the operations in reverse order, as strange as that may seem. Instead of starting with a single tree representing the string "$\texttt{a}$", we store $26$ trees. The $i$-th tree represents the final string if we started with only the $i$-th lowercase character. This allows us to merge large trees together efficiently when processing each operation.
Using these two ideas, we can construct an efficient, linear-time solution. The analysis of the runtime is as follows:
Constructing all the trees can be done in linear time because merging two trees happens in constant time, and we merge two trees each time we process a single character in the input. Let $M = r - l + 1$ and $N$ be the number of operations. When we traverse the binary tree, there are three categories of nodes we encounter:
To prevent integer overflow in languages like C++ and Java, we need to cap subtree sizes at $10^{18}$. This works because we never care about the contents of $S$ beyond the $10^{18}$-th character.
My C++ code:
#include <algorithm>
#include <iostream>
#include <string>
#include <utility>
typedef long long ll;
using namespace std;
const ll INF = 1e18;
struct Node {
char value;
ll size;
Node *l, *r;
void print_substring(ll start, ll end) {
start = max(start, 1ll);
end = min(end, size);
if (start > end) {
return;
}
if (value != '.') {
cout << value;
} else {
l->print_substring(start, end);
r->print_substring(start - l->size, end - l->size);
}
}
};
Node* current[26];
pair<char, string> operations[200000];
int main() {
cin.tie(0)->sync_with_stdio(0);
ll l, r;
int n;
cin >> l >> r >> n;
for (int i = n - 1; i >= 0; i--) {
cin >> operations[i].first >> operations[i].second;
}
for (char c = 'a'; c <= 'z'; c++) {
current[c - 'a'] = new Node{c, 1};
}
for (int i = 0; i < n; i++) {
Node* result = nullptr;
for (char c : operations[i].second) {
Node* to_merge = current[c - 'a'];
if (result == nullptr) {
result = to_merge;
} else {
result = new Node{
'.',
min(INF, result->size + to_merge->size),
result,
to_merge
};
}
}
current[operations[i].first - 'a'] = result;
}
current[0]->print_substring(l, r);
cout << '\n';
return 0;
}
Note that it's very important that leaf nodes only contain individual letters and not empty strings. Changing the one line
Node* result = nullptr;
to
Node* result = new Node();
results in an $\mathcal O(NM)$ solution instead because the empty string gets repeated many times in $S$ but doesn't count toward its length.
Danny Mittal's Java code:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;
public class FindAndReplace {
public static final long MAXVAL = 1000000000000000000L;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer tokenizer = new StringTokenizer(in.readLine());
long l = Long.parseLong(tokenizer.nextToken());
long r = Long.parseLong(tokenizer.nextToken());
int amtOperations = Integer.parseInt(tokenizer.nextToken());
List<Operation> operations = new ArrayList<>();
for (; amtOperations > 0; amtOperations--) {
tokenizer = new StringTokenizer(in.readLine());
char before = tokenizer.nextToken().charAt(0);
char[] after = tokenizer.nextToken().toCharArray();
operations.add(new Operation(before, after));
}
BigString[] currs = new BigString[26];
for (char chara = 'a'; chara <= 'z'; chara++) {
currs[chara - 'a'] = new BigString(true, chara, null, 1);
}
Collections.reverse(operations);
for (Operation operation : operations) {
if (operation.after.length == 1) {
currs[operation.before - 'a'] = currs[operation.after[0] - 'a'];
} else {
BigString[] elements = new BigString[operation.after.length];
long length = 0;
for (int j = 0; j < elements.length; j++) {
elements[j] = currs[operation.after[j] - 'a'];
length += elements[j].length;
length = Math.min(length, MAXVAL);
}
currs[operation.before - 'a'] = new BigString(false, '\0', elements, length);
}
}
StringBuilder out = new StringBuilder();
currs[0].append(l, r, out);
System.out.println(out);
}
static class Operation {
final char before;
final char[] after;
Operation(char before, char[] after) {
this.before = before;
this.after = after;
}
}
static class BigString {
final boolean isSingleton;
final char chara;
final BigString[] elements;
final long length;
BigString(boolean isSingleton, char chara, BigString[] elements, long length) {
this.isSingleton = isSingleton;
this.chara = chara;
this.elements = elements;
this.length = length;
}
void append(long from, long to, StringBuilder builder) {
from = Math.max(from, 1);
to = Math.min(to, length);
if (from <= to) {
if (isSingleton) {
builder.append(chara);
} else {
long curr = 0;
for (BigString element : elements) {
element.append(from - curr, to - curr, builder);
curr += element.length;
curr = Math.min(curr, MAXVAL);
}
}
}
}
}
}