The naive solution for this problem would be to iterate over all possible $\binom{n}{3}$ lots, then count the number of points that fall within each lot. However, this solution takes $O(n^4)$ time, which is a bit too slow.
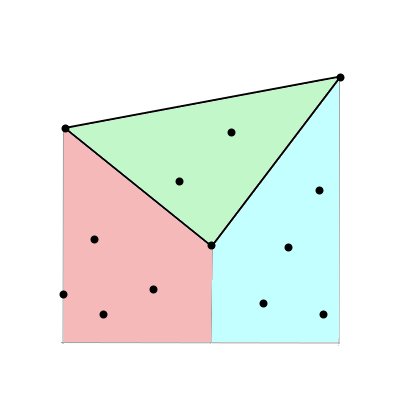
Since $n$ is fairly small, we need only improve this solution by a factor of $n$ to get full credit. One way we can do this is by simplifying the last step, where we count the number of points contained in each lot. Intuitively, a point is contained within a lot if, and only if, it is directly "below" one line making up the boundary of the lot and directly "above" another line. More specifically, we can think of each lot as being divided up as in the following picture:

This helps us because the number of points in the green triangle is equal to the number of points below the top line, minus the number of points below the bottom two lines. Since there are $O(n^3)$ different possible lots but $O(n^2)$ possible lines, this suggests a faster solution. For any line that can make up one side of a lot, we can precompute the number of points below this line in $O(n^2 \cdot n)$ time. We can then iterate over each possible lot as before. However, we can now compute the number of points faster than $O(n)$ per lot: we do so by iterating clockwise around the lines that make up the triangle. For each line, we either add or subtract the number of points under the line, depending on whether the line is a top or bottom edge of the triangle.
This subprocedure is $O(1)$, so the second iteration over all lots is $O(n^3)$ as well. The algorithm as a whole is therefore also $O(n^3)$, which is fast enough to receive full credit.
Richard Peng's solution is below:
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <complex>
using namespace std;
#define FR(i, a, b) for(int i = (a); i < (b); ++i)
#define FOR(i, n) FR(i, 0, n)
#define MP make_pair
#define A first
#define B second
typedef long long ll;
typedef complex<ll> pnt;
const int MAXN = 400;
#define X real
#define Y imag
pnt lis[MAXN];
int n;
int num[MAXN][MAXN];
int ans[MAXN];
ll cross(pnt a, pnt b) {
return imag(conj(a) * b);
}
pnt getPoint() {
int x, y;
scanf("%d%d", &x, &y);
return pnt(x, y);
}
int below(int i, int j) {
return (X(lis[i]) == X(lis[j])) && (Y(lis[i]) < Y(lis[j]));
}
int betweenBelow(int i, int j, int x) {
if (X(lis[i]) < X(lis[j])) {
return X(lis[i]) < X(lis[x]) && X(lis[x]) < X(lis[j]) &&
cross(lis[j] - lis[i], lis[x] - lis[i]) < 0;
} else {
return X(lis[j]) < X(lis[x]) && X(lis[x]) < X(lis[i]) &&
cross(lis[i] - lis[j], lis[x] - lis[j]) < 0;
}
}
int main() {
scanf("%d", &n);
FOR(i, n) {
lis[i] = getPoint();
}
memset(num, 0, sizeof(num));
FOR(i, n) {
FOR(j, n) if(X(lis[i]) < X(lis[j])){
FOR(k, n) if(k != i && k != j) {
if(below(k, i)) num[i][j]++;
if(below(k, j)) num[i][j]++;
if(betweenBelow(i, j, k)) {
num[i][j] += 2;
}
}
num[j][i] = -num[i][j];
}
}
memset(ans, 0, sizeof(ans));
FOR(i, n) FOR(j, i) FOR(k, j) {
int temp = abs(num[i][j] + num[j][k] + num[k][i]) / 2;
temp -= betweenBelow(i, j, k);
temp -= betweenBelow(j, k, i);
temp -= betweenBelow(k, i, j);
ans[temp]++;
}
FOR(i, n - 2) {
printf("%d\n", ans[i]);
}
return 0;
}